これで上司も市民も納得! 基礎からの統計教室
(1)151105平均値に気をつけろ
例題
あなたは就職試験を受けることになりました。A社のパンフレットには全社員の平均年収は600万円となっています。B社も同じく600万円ですが、巷では安い給料で働かされていると噂されています。A社、B社とも業務内容や社員数は同じです。面接で給与のことを聞きたいのですが、あなたはどんなことを聞きますか。
解説
年収が高いのは誰にとっても魅力です。年収600万ならかなり裕福な生活が出来ます。A社もB社も給料だけ見れば600万円で、なぜB社に悪評が立つのか分かりません。
実は、ここに平均値の落とし穴があります。
1.簡単なモデルを作って考えてみる
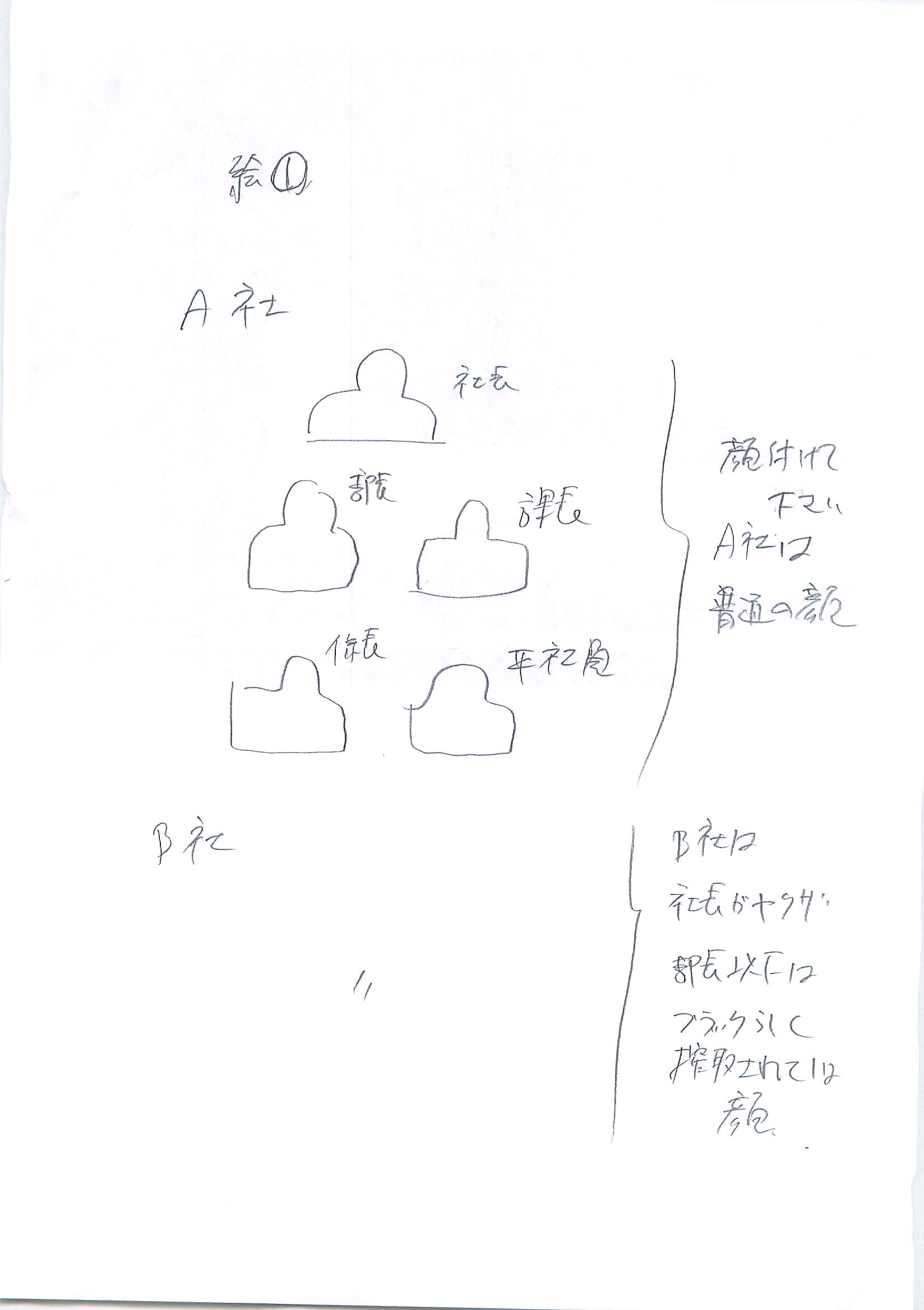
話を簡単にするために、社員は5人だけとします(絵1)。
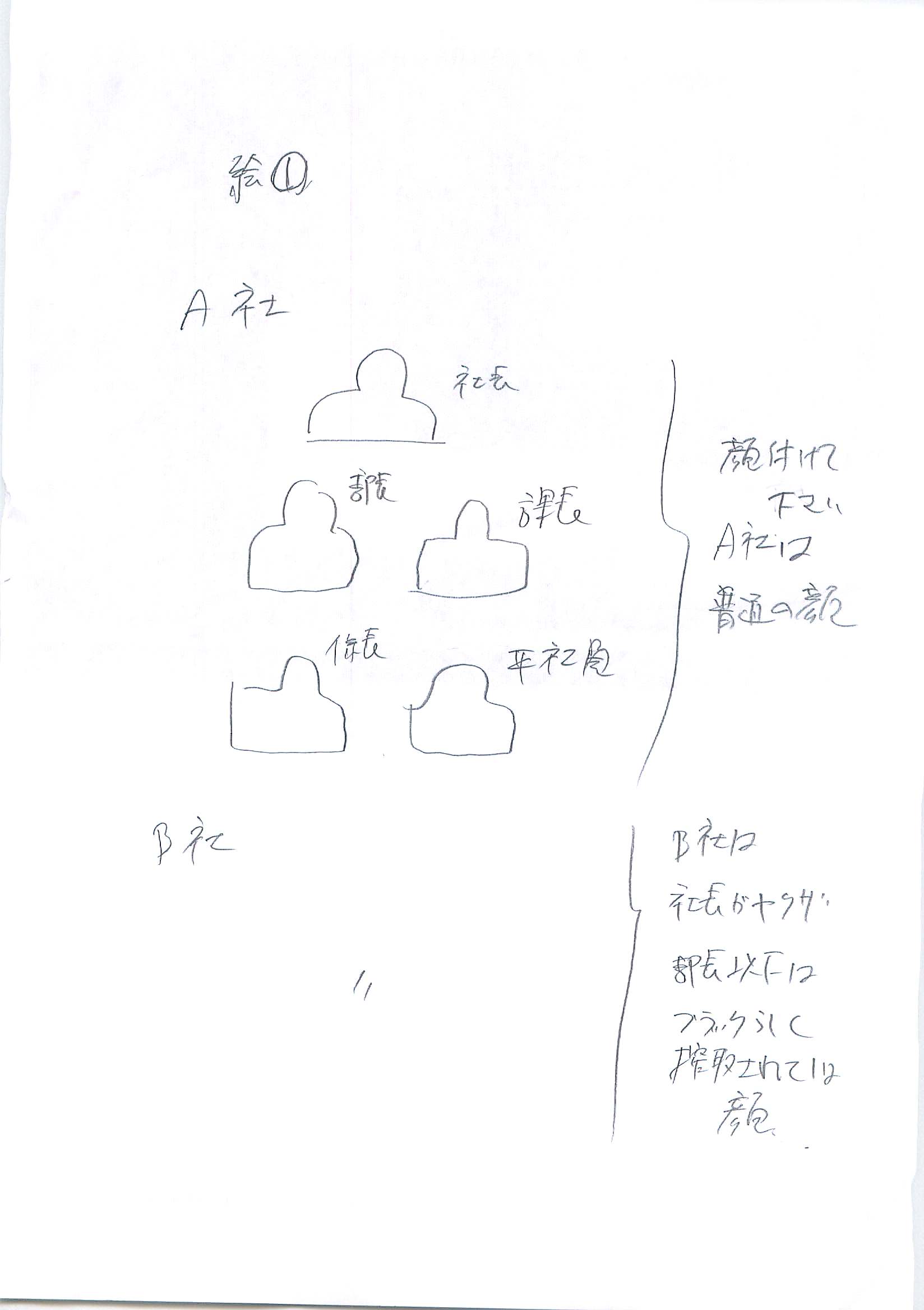
A社は
社長
部長
課長
係長
平社員
悪評のあるB社も
社長
部長
課長
係長
平社員
この人たちの平均年収は
A社は600万円
B社は600万円
です。
ここまでは全く同じですね。
ところが個人個人の年収は(絵2)
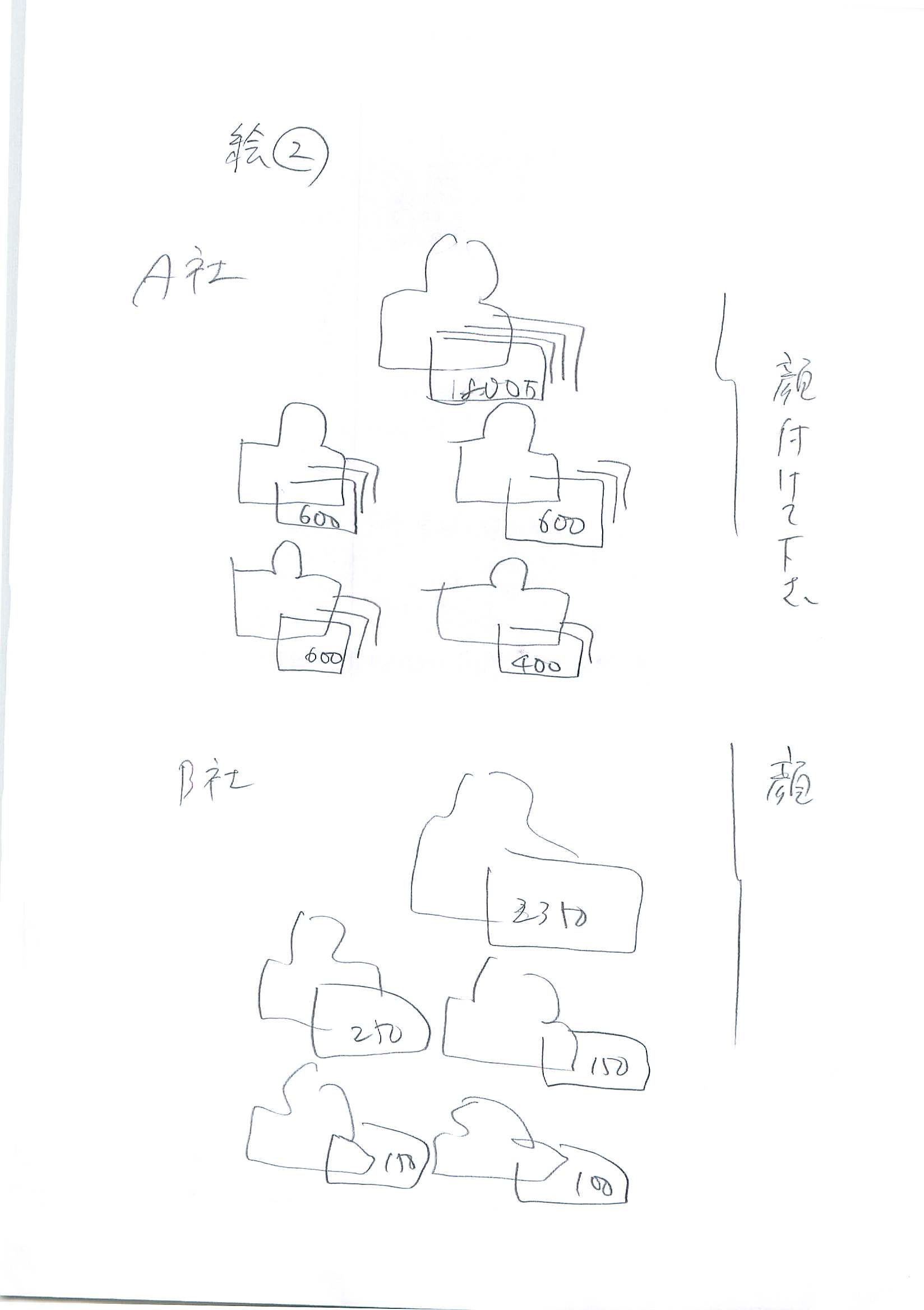
A社
社長800万円
部長600万円
課長600万円
係長600万円
平社員400万円
B社
社長2350万円
部長250万円
課長150万円
係長150万円
平社員100万円
でした。どちらも年収総額は3000万円、5人で割れば平均年収は600万円です。もしあなたがB社に就職したとしても、社長にならない限りA社の平社員の給料に追いつきません。B社が一族経営でしたらあなたが社長になる可能性はゼロです。
平均値だけではなぜB社の評判が悪いかは分かりません。それは、平均値は一つの極端な値によって影響を受けるからです。これが平均値の最大の欠点です。平均値が信用できるのは値の広がりが富士山のように上下左右均等に広がっている場合(正規分布)に限られます(絵3)。
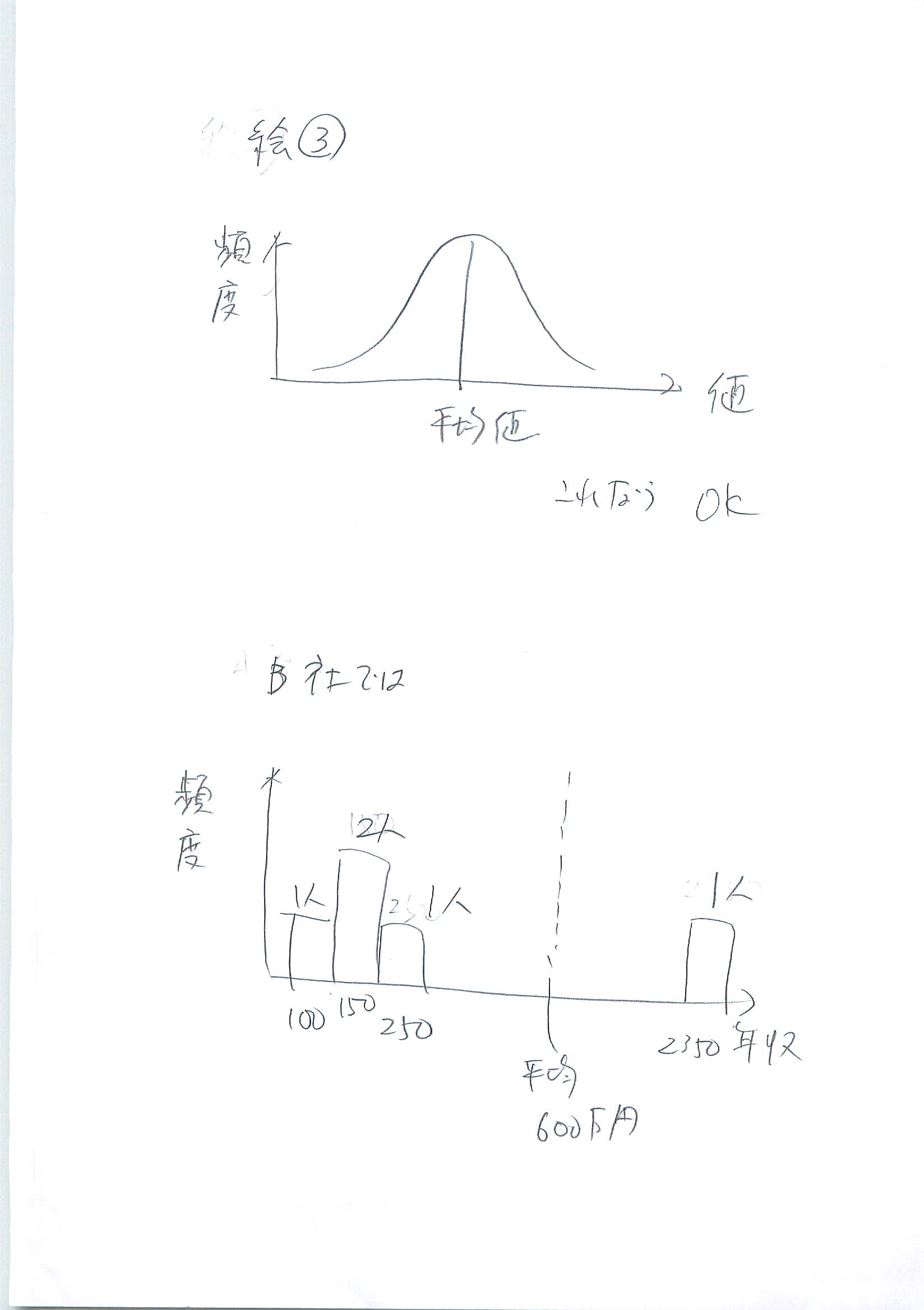
2.もっと分かりやすい表現を考える
それでは平均値以外で年収を表す方法を考えてみます。
最も確実なのは生のデータを示すことです。ですが、5例くらいなら可能でしょうが、これが何千、何万となると書く人も大変ですし、見る人もいなくなります。
そこで、昔の偉い人たちは考えました。
1)中央値(絵4)
一連の値を大きい順に並べます。その真ん中の人の値が中央値です。
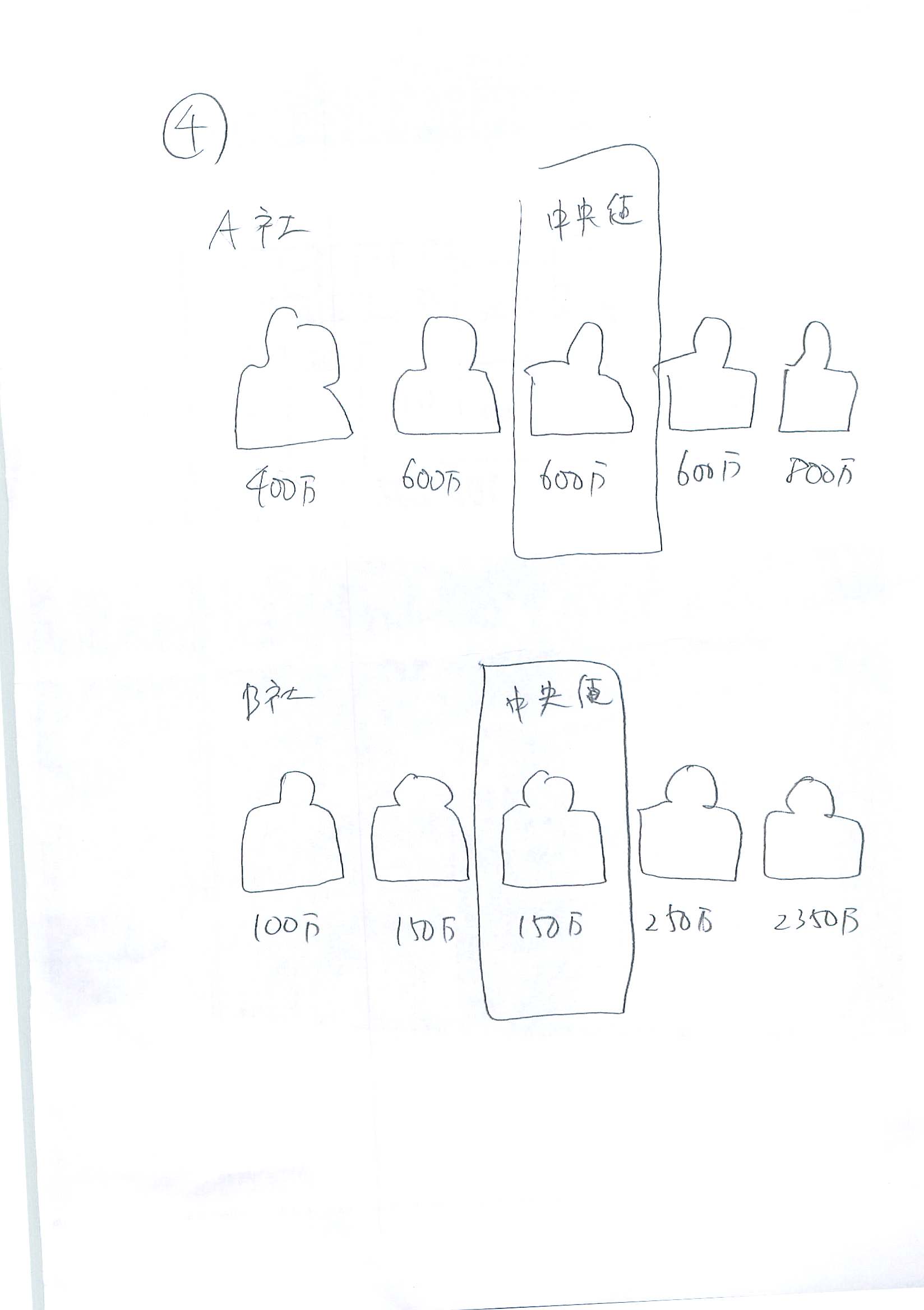
例の2社の場合は
A社
600万円
B社
200万円
これなら、A社の方がいい給料をもらえるのが分かるでしょう。中央値は極端な値を無視できるので、差の激しい群を代表させる時に使います。
2)最頻値(絵5)
一連の値のうち、最も良く出現する値のことを言います。
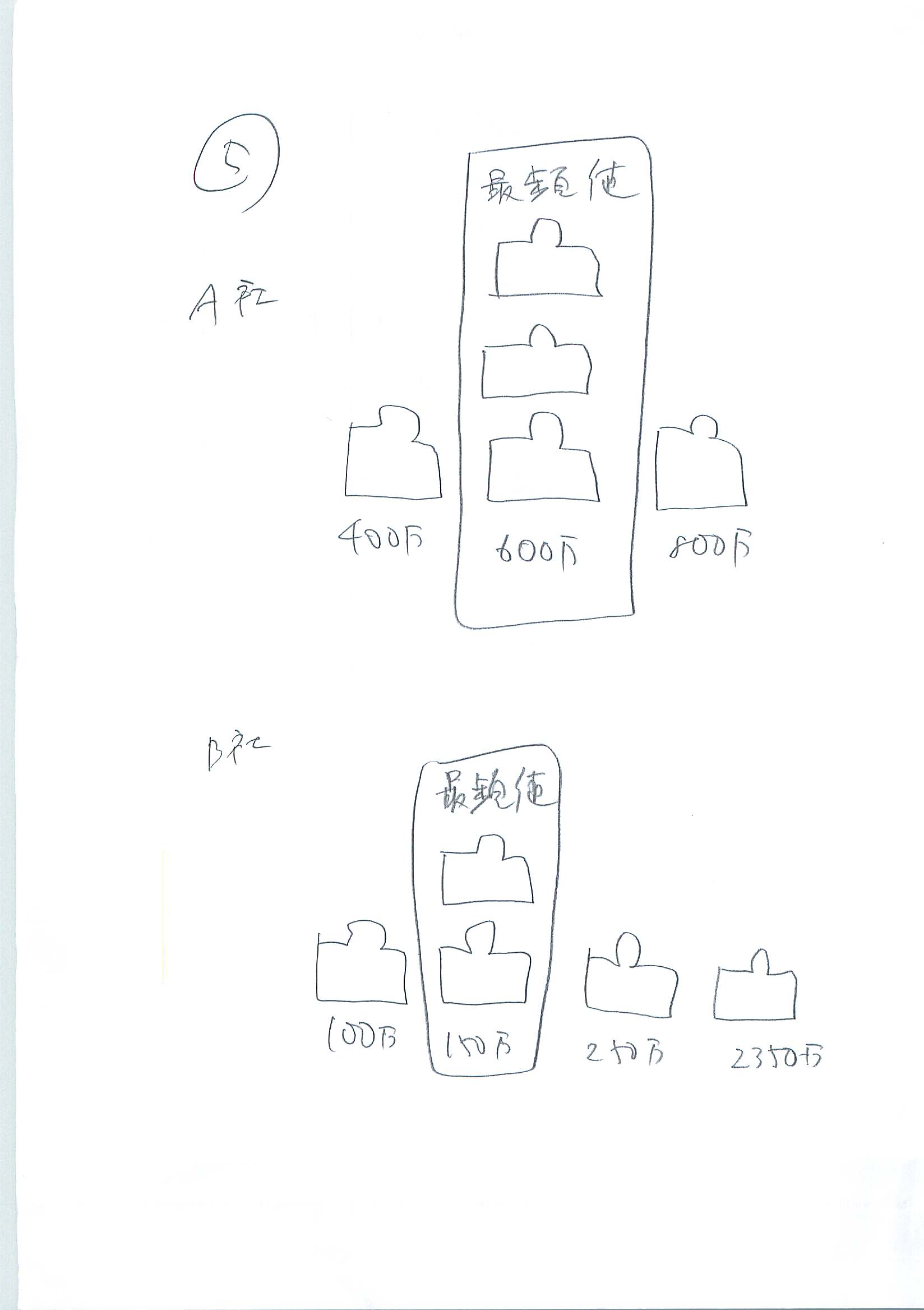
A社
3人が600万円
B社
2人が150万円
これを見ると、A社は裕福な人が多く、B社は貧乏な人が多いことが分かります。集団の性質を知る有力な情報となります。
2)最大値と最小値(絵6)
読んだ通りの値です。
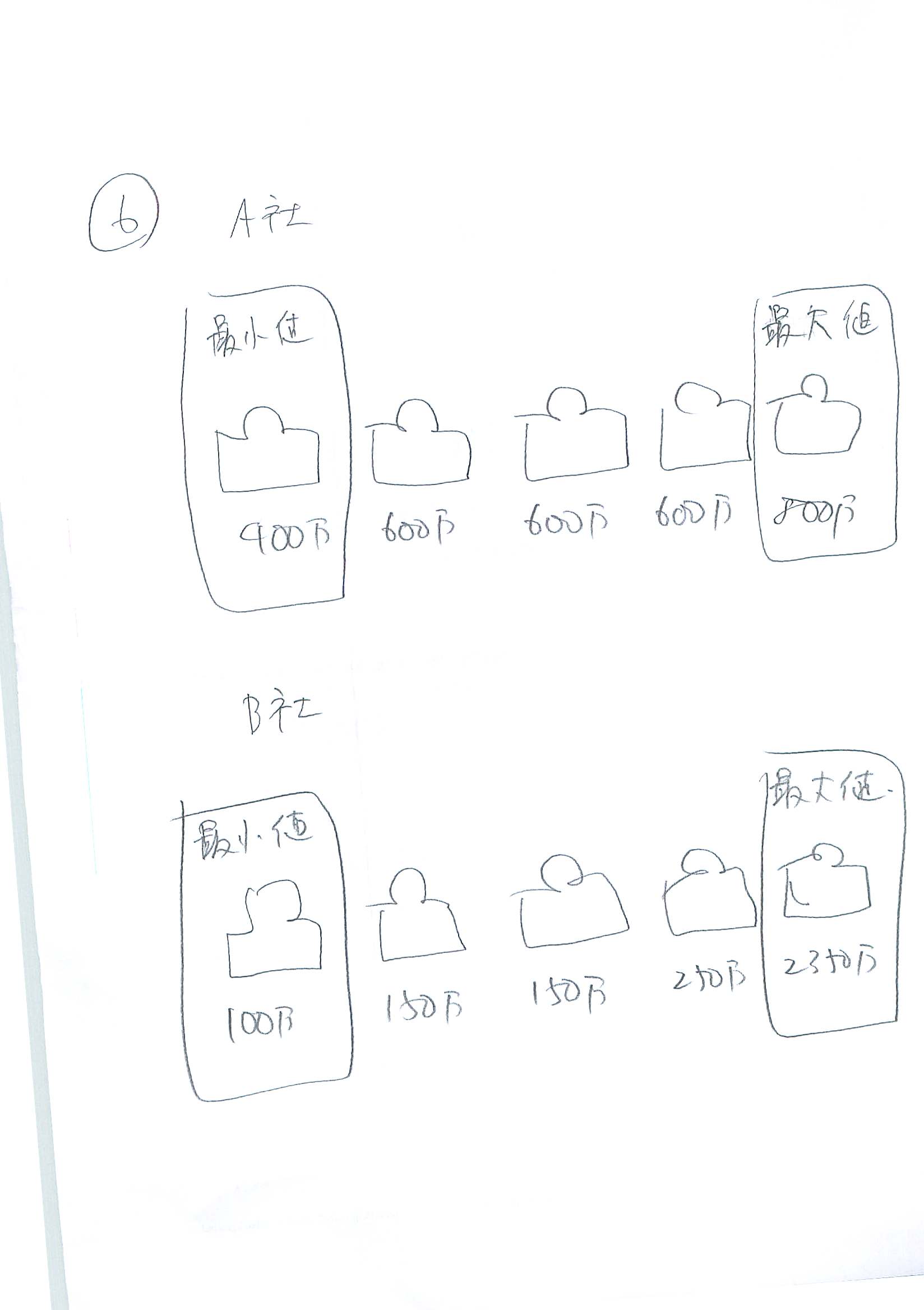
A社
最大値:800万円
最小値:400万円
B社
最大値:2350万円
最小値:100万円
最大値・最小値をみると、A社は日本型もしくは公務員(平等)型、B社はアメリカ型もしくは成果主義型だと分かります。どちらを選ぶかはあなたの価値観次第です。
3.日本全体の年収では
2009年の統計では、平均年収は549万円、中央値は438万円です。最頻値は200万から300万円です。最小値は当然0円ですが、最大値は所得番付が発表されていないので分かりません。
中央値より平均値が高いのは、所得が低い人が多く、所得が高くなるに連れて人数が減っていく、岩手山のような分布になっているからです。
4.答
面接では、初任給や手当ての内容を聞いてみましょう。平均値が分かっていればそれでおおよその給与体系は想像できます。
5.まとめ
・平均値が信用できるのは富士山のようなデータの時だけ。
・平均値以外にも集団の性質を示す値がある。
15.11.5/5:03 PM


コメント